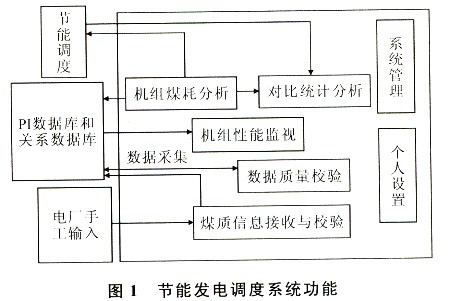
第 38 卷 第 19 期电 力 系 统保 护 与 控 制Vol.38 No.19 2010 年 10 月 1 日Power and . 1, 2010 电力市场环境下独立发电商的机组优化调度 常文平1, 2， 罗先觉1 （ 1. 西安交通大学电气工程学院， 陕西 西安 ； 2. 河南机电高等专科学校， 河南 新乡 ） 摘要： 针对火电机组的煤耗特性随着发电机的运行状况不断变化的特点， 在满足发电运行的各种约束条件下， 综合考虑发电会计成本， 提出了 电力市场环境下基于两部制电价成本的优化调度模型。 根据独立发电商发电机数量较少和实际运行的特点，利用改进动态规划法, 通过减少机组运行状态组合对其快速求解。 采用 上述模型对采用 两部制电价的某电厂进行了 仿真计算，结果表明该模型可明显提高大功率发电机组利用 率， 对节能减排和高效设备投资具有引 导作用 。 关键词: 优化调度； 电力市场； 独立发电商； 两部制电价； 节能减排 model of power units in CHANG Wen-ping1,2， LUO Xian-jue1 (1. of , Xi’an , Xi’an ， China； 2. Henan and , , China ) : As to the of coal of coal- units with state, on that kinds of of are ， this paper an model based on two-part price cost under , in which cost of power plant is . to the of power and its state, an which the is . is made using the above model on an power plant which two-part price cost. It is shown that the model can the rate of high-power and has a role in -, and of - . Key words: ； ； power ； two-part price； - and 中图分类号： TM734 文献标识码： A文章编号： 1674-3415(2010)19-0102-050 引言 在增加很少投资的条件下， 机组优化调度就能获得较大的经济效益和社会效益， 根据相关资料和华北、 东北等电网的实际测算， 通过优化调度节省能源可达总耗量的0.5%～1.5%[1-2]。

文献[3-4]介绍了集中调度下电力系统机组组合和优化调度的数学模型和方法， 其中的目标函数为机组的燃料费用， 随着电力工业市场化的改革， 这已经不能适应电力市场的要求[5]， 目标函数更多转变为购电成本或社会总收益[6-9]。 在诸多方法中， 对于给定的发电机组，发电机的燃料消耗或燃料费用函数方程采用固定的二次曲线表示， 这不符合生产实际情况， 事实上，随着发电机运行年限的增加和维修效果的不同电力节能减排论文， 发 基金项目： 河南省中青年骨干教师资助项目（ -134） 电机的耗量特性参数也逐渐变化， 同时， 由于大量的发电机的实际运行范围比较小， 使得测试发电机变化后的耗量特性参数非常困难， 导致按照发电机的固定耗量特性参数计算最优解偏离实际最优解较大， 从而影响发电机组的优化调度效果。 针对这种情况， 本文使用生产实际中经常测试的发电量费用、空载旋转费用（对应容量费用） 以及机组启动费用，建立基于两部制电价的数学模型， 在独立发电商通过竞价获得日前发电计划后， 使得该目标函数最小。由于独立发电商的发电机数量比较少， 并根据实际发电机组运行的特点， 采用改进的动态规划法，通过大量减少机组运行状态的组合快速求解。

最后对使用两部制电价的某电厂试验， 并与该厂实际运行结果对比， 取得了 满意的效果， 表明本文提出的方法具有可行性和有效性。常文平， 等 电力市场环境下独立发电商的机组优化调度- 103 - 1 机组组合的数学模型 1. 1 独立发电商日 前发电计划的获得 在电力市场环境中， 发电商首先要采用多种方法预测次日各时段市场实时电价[10-14]， 在尽可能准确预测电价的基础上， 发电商制定自己总的电量-价格竞价曲线， 并提交电力交易中心， 如图1所示。 电力交易中心将发电商的竞价曲线和用户的需求曲线进行匹配， 形成各独立发电商次日各时段的发电量，假设实时电价按小时出清电力节能减排论文， 并且获得的出清电量在数值上等于发电功率， 形成独立发电商的发电计划， 发电商根据自己机组的状况进行机组组合和负荷优化分配。 发电量/价格/($/MWh) 图1 独立发电商竞价曲线 Fig.1 Bid curve of power 1 . 2 目 标函数 在两部制电价环境下， 独立发电商通过竞价获得日 前发电计划后再进行机组组合， 其目 标是使发电费用、 空载旋转费用（对应容量费用） 以及机组启动费用最小。

设研究的总时段数为T， 机组数量为N， 则机组组合问题的目 标函数为： ]gs=1 =1∑∑min=( )( )( ))+( )(1u t(1)) t C P t + u t Cu tS⎡⎣-- (1)式中：式中： Pi(t)是机组i在时段t的出力；( )iu t 为机组i的工作状态，( )=1iu t表示机组i在时段t处于运行状态，( )=0iu t表示机组i在时段t处于停机状态；g i C 为机组i的每MWh的发电费用；s i C 为机组i的空载旋转费用；1 . 3 约束条件 1） 系统负荷平衡约束 iS 为机组i启动费用。 d1( )( )Niip tp t==∑ 1,2,,tT∀ =⋅⋅⋅ (2) 式中，d( )P t 为发电集团或独立发电商在电力市场通过竞价获得的发电功率， 其获得方法如前所述。 2） 系统备用约束 maxdr=1(( ) ( ))it u t( )( ) tP t ≥∑-- （3） 1,2,,tT∀ =⋅⋅⋅ 式中：max( )iPt 为发电机组 i 在第 t 小时的最大输出功率；r( )P t 为电力系统在第 t 小时的备用容量。

3） 发电机组的输出功率限制 ( )iiiPP tP≤≤ 1,2,,tT∀ =⋅⋅⋅ （4） 式中：maxiP为发电机组 i 的最大输出功率；miniP为发电机组 i 的最小输出功率。 4） 发电机组的最小启停时间限制 up1( )iiX tT≤≤， ui(t)=1（5） 式中： Xi(t)为发电机组 i 在第 t 小时的状态变量， 为正值表示该机组目前处于开启状态， 并且已经运行了 Xi(t)小时；upiT为发电机组 i 的启动时间， 在此段时间内不能停机。 dn( )1iiTX t−≤≤ − , ui(t)=0（6） 式中： Xi(t)为负值表示该机组目前处于关闭状态，并且已经关闭了-Xi(t)小时；dniT为发电机组 i 的关闭时间， 在此段时间内不能开机。 5） 机组爬坡约束限制 这里假设机组出力增加速度和减少速度相同。 ,1Riti tiPP−−≤ Δ（7） RiΔ为机组i的出力爬坡限制。 2 求解算法 机组优化调度的算法有启发式方法、 优先顺序法、 整数规划和混合整数规划法、 动态规划法、分支定界法、 拉格朗日 松弛法、 专家系统法、 模拟退火算法、 人工神经网络法、 遗传算法等[15-16]，考虑到动态规划法对目 标函数没有特殊的要求，能求得全局最优解， 同时， 对于独立发电商的发电机组数量较少的特点， 本文采用改进的动态规划算法。

2. 1 删除不可能存在的机组组合状态 如果使用完全状态的动态规划法, 对于N台机组、 T个时段的机组组合,总的机组状态组合数量可- 104 -电 力 系 统保护与控制 以达到（2N –1）加， 形成所谓“维数灾” 问题。 为了克服“维数灾”问题， 根据机组组合的实际情况， 除掉不可能的组合状态。 1) 删除发电功率不符合要求的组合状态 根据发电功率平衡要求， 删除每一个时段处于“运行” 状态的机组的最小功率之和仍大于负荷需求功率的组合； 删除每一个时段处于“运行”状态的机组的最大功率之和仍小于负荷需求功率的组合。 2) 删除机组启 停费用高于发电收益的组合状态 在满足机组发电的物理约束条件下， 删除机组启停费用高于发电收益的组合状态。 3) 删除机组启 停时间不符合要求的组合状态 以拥有4台机组10个小时机组调度为例， 假定调度周期内旋转备用容量为50 MW， 说明删除不符合要求的机组组合方式。 表1、 表2分别为发电机和负荷的参数， 表3为机组组合状态表。 在表3中， 折线下面为功率不符合要求的组合状态； 椭圆内部的两种组合状态中， #3和#4发电机的停机时间为1 h， 不满足最小停机时间要求， 应当去掉。

通过删除不符合功率要求的组合状态， 没有运行效益甚至运行效益为负的组合状态， 以及启停时间不符合要求的组合状态， 可以使组合状态明显减少， 从而提高计算效率。 T, 当N和T增大时， 计算量急剧增表1 机组参数 Tab.1 The of four units Unit No. 1 2 3 4 Pmax/MW 300 200 135 55 Pmin/MW 180 120 80 30 Tup/h 6 5 5 3 Tdn/h 4 3.5 3 2 表2 负荷数据 Tab.2 Load for four 10 hours Hour 1 2 3 4 5 Load/MW 390 450 500 550 620 Hour 6 7 8 9 10 Load/MW 600 540 480 510 520 2. 2 递推公式 动态规划计算过程分为正序造表和逆序查表两大步。 在计算过程中， 一般选取时段t为阶段变量， 第t+1时段的机组组合号J为状态变量， 第t时段的机组组合号j为决策变量， 状态转移方程为f(t,j)=J*， 则动态规划最优化递推计算式为： {}**( , )min( , )+ ( , )+d t k( +1, )J titJ t kS j kk= (8) s.t *( , )J t k 为t时段k号组合下从t时段到末时段( , )*( ,)=f t jJ(9) 式中：T最小总发电运行费用；id t k 为t时段k号组合下发电运行费用；( , )tS j k 为t+1时段j号组合转移到到t时段k号组合的机组启动费用。

表3 机组组合状态曲线 Tab.3 The for unit 时间/h 编号机组组合最大功率/MW12 3 4 5 6 789 ** * * * * **** ** * * * * ****** * * * * ****** * * * * ****** * * * * ****** * * * * ****9 ** * * * * **** 8 ** * * * * **** 7 ** * * * * **** 6 ** * * * * **** 5 ** * * * * **** 4 ** * * * * **** 3 ** * * * * **** 2 ** * * * * **** 1 ** * * * * **** 0 00000 ** * * * * **** 3 算例 以实际电网中某发电公司有关机组的参数为基础， 对具有6台火电机组的系统进行机组组合的优化计算。

该发电公司装有6台发电机， 某典型日各发电机的参数见表4， 其中#1、 #2发电机没有安装脱硫装置， #3、 #4发电机采用配套的高压再热循环硫化床（CFB） 锅炉， #5、 #6发电机配套有烟气脱硫装置。 通过集中竞价， 电厂内部优化次日 24 h各时段的发电功率如表5所示。 分两种情况优化各机组的发电负荷。 Case1. 不考虑排污收费 在6台发电机中， #1、 #2发电机没有安装脱硫设备， 在不考虑排污收费的情况下， 优化调度结果如表5所示， 发电费用为573.4万元， 比典型日对应财务成本低3.2万元， 节约费用约0.56%， 经济效益明显。常文平， 等 电力市场环境下独立发电商的机组优化调度- 105 - 表4 机组的特性参数 Tab.4 The of unit 机组 Pmin/ MW 100 100 70 70 150 150 Pmax/ MW 220 220 135 135 320 320 S/ (万元) 20 20.3 11 11 27.5 27.5 CS/ (元/h) 2 600 2 500 1 900 1 800 3 000 3 000 Cg/ (元/MWh) 126 124 130 129 114 112 Tdni/ h 8.5 8.5 12 12 24 24 Tupi/ h 10 10 12 12 16 16 PR/ (MW/m) 3 3 2 2 5 5 #1 #2 #3 #4 #5 #6 Case2. 考虑排污收费 考虑对#1、 #2 发电机污染物排放收费， 假设收费标准为 20 元/MWh， 这种情况下的优化调度结果如表 5 所示， 从优化结果可以看出#1、 #2 发电机出 力和发电量明显下降， 从 6 440 MWh 下降到5 155 MWh， 下降约 20%， 这有利于减少硫化物和氮化物的排放。

表 5 两种情况的优化调度结果对比 Tab.5 of in case 1and case 2 #1 机功率/MW #2 机功率/MW #3 机功率/MW #4 机功率/MW #5 机功率/MW #6 机功率/MW 时 段 负荷/ MW Case1 Case 2 Case1 Case Case Case Case 2 Case1 Case 21 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 870 890 880 870 870 870 1 000 1 050 1 250 1 100 1 100 1 080 1 080 1 100 1 070 1 060 1 050 900 1 200 1 180 1 150 1 000 910 950 100 100 100 100 100 100 100 100 170 100 100 100 100 100 100 100 100 100 170 180 150 100 100 100 100 100 100 100 100 100 100 100 170 100 100 100 100 100 100 100 100 100 143 100 100 100 10...

相关热词 : 电力节能减排论文 电力节能政